1. 트리
트리는 그래프 중 하나로 그래프와 같이 노드와 엣지로 구성되어 있다. 한 노드가 여러노드를 가리킬 수 있으며, 비선형적인 자료구조이다.
데이터 구조의 계층적인 속성을 표현하는 것이 특징이다. 우리가 사용하는 파일탐색기의 구조도 트리 구조라고 볼 수 있다.

Tree를 알아보기에 앞서 트리와 관련된 용어를 알아야 할 필요가 있다.
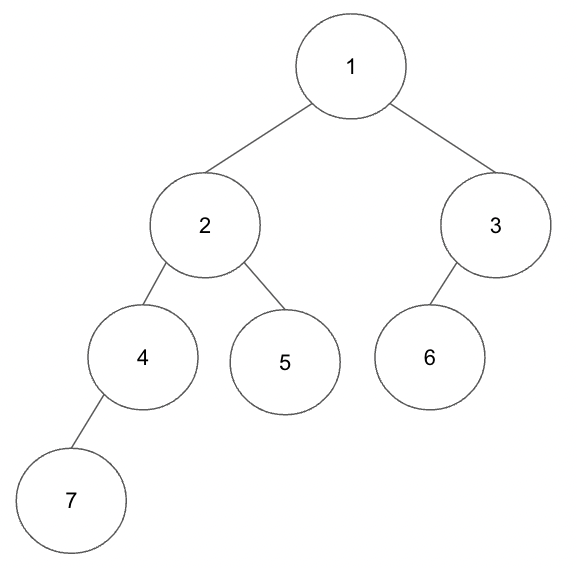
1. Root: 트리의 시작점이자, 트리에서 제일 위에 있는 최상위 노드이다. 이를 root라고 부른다.
2. Node와 Edge: 노드는 트리에서 데이터를 저장하는 기본적인 단위이다. 각 노드는 하나이상의 자식노드를 가지고 있을 수 있고, 또한 부모노드와 연결될 수도 있다. 그리고 노드들을 연결해주는 간선을 Edge라고 한다.
3. Parent와 Child: 그림에서는 2번노드가 부모 6번노드가 자식이라고 표현되어 있듯이, 상위노드가 부모가 되고, 하위노드가 자식이 된다.
4. Leaf: 트리는 루트노드, 내부 노드, 리프노드로 이루어져 있는데, Leaf노드는 자식이 없는 트리의 맨 마지막에 있는 노드를 의미한다.
5. Degree: 노드에 연결된 노드의 갯수가 Degree를 결정한다. 그림에서 루트노드의 차수는 3이다.
트리에는 이진트리, AVL, 레드블랙트리 등 여러종류가 존재한다.
2. 이진트리
이진트리는 각 노드가 최대 2개의 자식노드를 가지는 트리이다. 이진 트리에도 여러가지 종류가 있다.
1) 정 이진트리(Full Binary Tree), 엄격한(strict) 이진 트리
모든 노드가 2개의 자식을 가지거나 아예 없는 경우

2) 포화 이진 트리(Perfect Binary Tree)
모든 노드가 2개의 자식을 가지고 모든 Leaf 노드가 같은 레벨인 경우

3) 완전 이진 트리(Complete Binary Tree)
마지막 레벨을 제외하고 모든 노드가 채워져야 하고, 노드는 왼쪽에서 오른쪽으로 채워져야한다.

4) 변질 이진트리(Degenerate Binary Tree)
자식노드가 하나밖에 없는 이진 트리

5) 균형이진 트리(Balanced Binary Tree)
왼쪽과 오른쪽 노드의 높이 차이가 1이하인 이진 트리. Map, Set을 구선하는 레드 블랙트리는 균형 이진트리 중 하나이다.
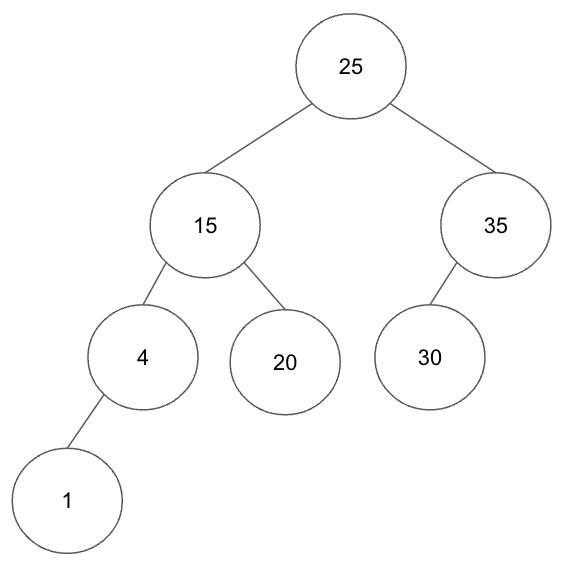
3) 이진 탐색 트리(BST)
이진 탐색 트리는 노드의 왼쪽 서브트리에는 현재 노드 보다 작은 값, 오른쪽 서브트리에는 현재 노드보다 큰 값이 들어 있는 트리를 말합니다. 중복값은 허용되지 않습니다.
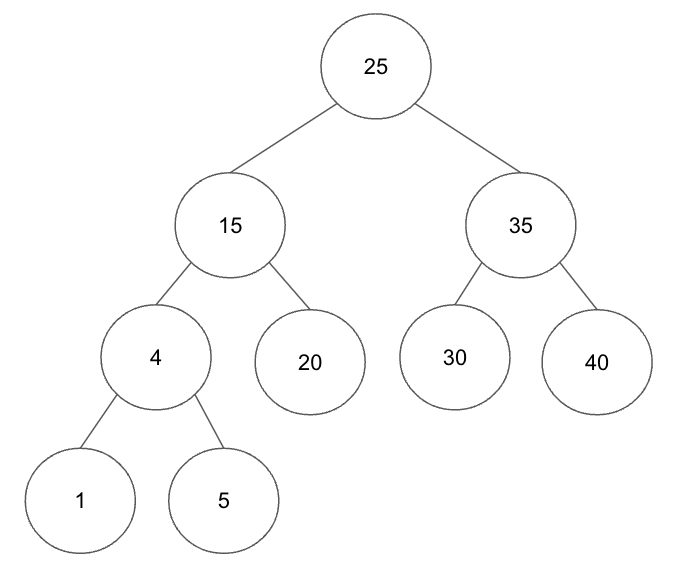
4) AVL 트리 (BST의 일종)
이진 탐색 트리는 최악의 경우 선형구조가 될 수 있는데, AVL 트리는 선형적인 트리가 되는 것을 방지하고 스스로 균형을 잡는 이진 탐색 트리이다. AVL 트리의 두 자식 서브트리의 높이는 항상 최대 1만큼 차이가 난다.
이진 탐색 트리가 선형적인 트리구조를 가질 때 최악의 경우 O(n)의 시간복잡도가 발생하는데 이런 최악의 경우를 배제하고 균형 잡힌 트리로 만들기 위해 등장한 개념이 AVL트리이다. 탐색, 삽입, 삭제 모두 시간복잡도가 O(logn)이며, 삽입,삭제가 발생할 경우 균형을 맞추기 위해 트리의 일부를 왼쪽이나 오른쪽으로 회전하면서 균형을 잡는 구조를 가지고 있다.
5) 이진 탐색 트리의 구현
트리의 기능을 명세한 인터페이스
insert: 값 삽입
delete: 값 삭제
contains: 값이 트리안에 존재하는지 확인
size: 엘리먼트의 갯수 확인
public interface ITree<T> {
void insert(T val);
void delete(T val);
boolean contains(T val);
int size();
}
이진탐색트리를 구현
package org.example.tree;
import java.util.ArrayList;
import java.util.List;
public class BinarySearchTree<T extends Comparable<T>> implements ITree<T> {
private Node root;
private int size;
public BinarySearchTree() {
this.root = null;
this.size = 0;
}
public T min() {
return this.minNode(this.root);
}
private T minNode(Node node) {
T minData = node.data;
while (node.left != null) {
node = node.left;
minData = node.data;
}
return minData;
}
public T max() {
return this.maxNode(this.root);
}
private T maxNode(Node node) {
T maxData = node.data;
while (node.right != null) {
node = node.right;
maxData = node.data;
}
return maxData;
}
@Override
public void insert(T val) {
this.root = this.insertNode(this.root, val);
this.size++;
}
private Node insertNode(Node node, T val) {
if (node == null) {
return new Node(val);
}
if (val.compareTo(node.data) < 0) {
node.left = insertNode(node.left, val);
}
if (val.compareTo(node.data) > 0) {
node.right = insertNode(node.right, val);
}
return node;
}
@Override
public void delete(T val) {
this.deleteNode(root,val);
}
private Node deleteNode(Node node, T val){
if(node == null){
return null;
}
if (val.compareTo(node.data) < 0){
node.left = deleteNode(node.left, val);
}
else if (val.compareTo(node.data)>0){
node.right = deleteNode(node.right,val);
}
else{
this.size--;
if(node.left == null){
return node.right;
}
else if(node.right == null){
return node.left;
}
// 끊어진 노드를 이어주는 방법으로는 왼쪽 서브트리의 최댓값을 가져와서 넣어주거나, 오른쪽 서브트리의 최솟값을 가져와 대입해주면 됨.
node.data = minNode(node.right);
node.right = deleteNode(node.right, node.data);
}
return node;
}
@Override
public boolean contains(T val) {
return containsNode(root, val);
}
private boolean containsNode(Node node, T val) {
if (node == null) {
return false;
}
if (val.compareTo(node.data) == 0) {
return true;
}
if (val.compareTo(node.data) < 0) {
return containsNode(node.left, val);
}
if (val.compareTo(node.data) > 0) {
return containsNode(node.right, val);
}
return false;
}
@Override
public int size() {
return this.size;
}
public List<T> preOrder() {
return this.preOrderTree(this.root, new ArrayList<>());
}
private List<T> preOrderTree(Node node, List<T> visited) {
if (node == null) {
return visited;
}
visited.add(node.data);
preOrderTree(node.left, visited);
preOrderTree(node.right, visited);
return visited;
}
public List<T> inOrder() {
return this.inOrderTree(this.root, new ArrayList<>());
}
private List<T> inOrderTree(Node node, List<T> visited) {
if (node == null) {
return visited;
}
inOrderTree(node.left, visited);
visited.add(node.data);
inOrderTree(node.right, visited);
return visited;
}
public List<T> postOrder() {
return this.postOrderTree(this.root, new ArrayList<>());
}
public List<T> postOrderTree(Node node, List<T> visited) {
if (node == null) {
return visited;
}
postOrderTree(node.left, visited);
postOrderTree(node.right, visited);
visited.add(node.data);
return visited;
}
class Node {
T data;
Node left;
Node right;
Node(T data) {
this.data = data;
}
Node(T data, Node left, Node right) {
this.data = data;
this.left = left;
this.right = right;
}
}
}6) 정리
트리는 비선형적인 자료구조이다. 데이터 구조의 계층적인 속성을 표현하는 것이 특징이다.
1. Root: 트리에서 제일 위에 있는 최상위 노드
2. Node와 Edge: 노드는 트리에서 데이터를 저장하는 기본적인 단위, 노드들을 연결해주는 간선을 Edge
3. Parent와 Child: 상위노드가 부모가 되고, 하위노드가 자식.
4. Leaf:Leaf노드는 자식이 없는 트리의 맨 마지막에 있는 노드를 의미.
5. Degree: 노드에 연결된 노드의 갯수가 Degree를 결정.
이진 트리의 종류로는
1. Full Binary Tree(Strict): 노드가 2개 있거나 아예 없음.
2. PerFect Binary Tree: 노드가 모두 2개.
3. Complete Binary Tree: 마지막 레벨을 제외하고는 모든 노드가 채워져야하며, 노드가 왼쪽부터 있어야 한다.
4. Degenerate Binary Tree: 자식 노드가 1개 씩 있다.
등등이 존재한다.
프로그래밍을 하기 위한 자료구조로는 이진탐색 트리를 기반으로 한 자료구조가 많이 쓰인다. (AVL, 블랙레드트리 등)
참조
면접을 위한 CS 전공지식 노트
야놀자 테크스쿨 패스트캠퍼스 온라인 강의 - 자료구조/알고리즘
'야놀자 테크스쿨 > JAVA 자료구조' 카테고리의 다른 글
| [자료구조] 힙과 우선순위 큐 (0) | 2023.08.10 |
|---|---|
| [면접을 위한 CS 전공지식 노트][자료구조] Graph (그래프) (0) | 2023.08.04 |
| [면접을 위한 CS 전공지식 노트][자료구조] Queue(큐) (0) | 2023.08.03 |
| [면접을 위한 CS 전공지식 노트][자료구조] Stack(스택) (0) | 2023.08.03 |
| [면접을 위한 CS 전공지식 노트][자료구조] 연결리스트 LinkedList (0) | 2023.08.02 |



